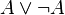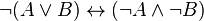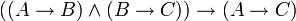Intelligence Artificielle
© Jean-Marc Vanel 2012 , licence Creative Common
Déductions SARL - Conseil, services,
formation.
Cette présentation utilise JavaScript, CSS et XHTML
via Slidy 2 du
W3C
Préambule : la connaissance et sa gestion
Qu'est ce que la connaissance?
Plusieurs choses:
- l'expertise : exemple "un béton contient des granulats
et un ciment"
- les algorithmes et formules : exemple "formule pour le
vieillissement d'un béton"
- les données : exemple "base de données sur les ciments
disponibles"
- un savoir faire plus ou moins explicité, exemple en
architecture, musique
- des documents bureautiques classés par sujets et multi-critères
Notre sujet sera : 1-2-3-4
Plan
Plan global
- Pourquoi l'IA est très importante, Les domaines de l'IA
- Modéliser la connaissance
- Logique formelle
- Web sémantique: vision, graphe d'objets URI, bases de données SPARQL,
Linked Open Data
- Notion d'ontologie , Logiques de Description , OWL
- Moteurs en chaînage avant RETE (alias moteurs de règles, systèmes de
production)
- Langages naturels contrôlés (CNL)
- Réutilisation de modèles, ontologies, vocabulaires, données
- De la connaissance au logiciel: différentes chaînes de traitement,
implémentation, déploiement
- Avantages par rapport à un développement classique
Plan partie 1 : introduction, logique
Pourquoi l'IA est très importante
L'avenir du développement logiciel
- Si vous aimez notre métier, et voulez faire une belle et intéressante
carrière, écoutez ceci.
- De puissantes forces économiques et techniques vont bouleverser la
façon de travailler en informatique
- D'un point de vue économique, les décideurs tolèrent de plus en
plus mal de payer très cher des fonctionnalités plutôt simples, ou
alors d'être dépendants de toutes sortes d'infrastructures et de
frameworks.
- D'un point de vue technique, on peut faire autrement avec l'IA
- Cependant , à l'heure actuelle le progrès n'est pas rapide:
- D'un point de vue technique, malgré un papillonnement de
nouveautés, il y a peu de concepts nouveaux.
- il faut attendre une génération pour que les développeurs passent
chefs
- Après les nouveautés de ces dernières années: Orienté Objet, XML,
Logiciel Libre, frameworks et Services Web, Cloud, nouveaux terminaux
- Ce qui va venir: la sémantique au premier plan: sémantiques métier et
celles de l'infrastructure aussi.
- ==> utiliser techniques issues de l'Intelligence Artificielle pour
gérer les développements et l'infrastructure.
- Plus que les développements off-shore, c'est cela qui va changer la
vie des développeurs.
- Bientôt, il n'y aura plus de postes de développement à "basse
technologie".
- les développements faisant appel à des compétences métiers, ce
seront les experts métiers qui les feront eux-même grâce à des
outils intelligents.
- Vous ne pourrez pas espérer rester en poste grâce à la maîtrise
d'un ou plusieurs frameworks (à moins d'en être l'auteur).
Les domaines de l'IA
- histoire : Aristote, les sophistes, Boole, Frege, Turing, résolution
de Robinson (1965), compétitions
annuelles des prouveurs
de théorèmes
- domaines :
- statistique, apprentissage automatique
- versus logique formelle:
- prouveurs de théorèmes et assistants
- moteur d'inférence, raisonneurs
- paradigme agents, cf le livre AIMA
( AI, a Modern Approach)
- succès: jeu d'échecs, reconnaissance images, son, robotique, prouveurs
de théorème (compilateur C, logiciels embarqués), indexation et fouille
de textes
- échecs:
AIMA: un manuel d'IA très utilisé dans le monde; des supports de
cours en Français .
Modéliser la connaissance : Logique métier et Système
d'Information
Le fil conducteur à travers les tendances du développement logiciel
pourrait être : comment on va (plutôt cahotiquement ) vers plus de
sémantique.
Domaines couverts par le logiciel d'entreprise:
| Domaine |
impacté par |
| 1 logique métier |
règles, langage Naturel Contrôlé |
| 2 IHM |
règles |
| 3 stockage persistant |
Web Sémantique |
| 4 échange de données |
Web Sémantique |
- Le point 1 est le parent pauvre, car dans le courant dominant
aujourd'hui, on code cela dans un langage procédural, typiquement
Java
- (ou alors on délègue ça à un progiciel comme SAP, ce qui revient
au même)
- langage procédural ( et non logique ) => non composable,
dépendance au langage
- Le point 4 est aussi un parent pauvre, car on pense en terme d'extraction
(ETL),
exportation et importation, le plus souvent en XML
Modéliser la connaissance : Formaliser, pérenniser, sécuriser
l'expertise métier
- pérenniser et sécuriser (afin qu'elle survive aux experts),
- formaliser, afin de pouvoir l'exécuter directement, la valider
- réutiliser pour construire du logiciel directement :
- plusieurs logiciels,
- pour plusieurs clients,
- sur plusieurs plateformes
- mais cohérentes car réutilisant la même logique
Logique des propositions - 1 - ingédients
cf Calcul_des_propositions
sur wikipedia
- les propositions atomiques, notées p, q, etc., qui
constituent généralement un ensemble infini dénombrable .
- Les deuxièmes constituants de base du langage du calcul des propositions
sont les opérateurs ou connecteurs :
| et |
∧ |
| ou |
∨ |
| non |
¬ ou ! |
| implique |
→ ou ⇒ |
| équivaut |
↔ ou ⇔ |
- la constante notée ⊥, prononcé taquet vers le haut[3], type
vide, bottom ou bot, qui vise à représenter le faux .
- on utilise des parenthèses pour lever les ambiguïtés dans les
formules
Logique des propositions - 2 - tables de vérité 1
cf "Calcul des propositions" sur Wikipédia, 2.2.1 Interprétation des
connecteurs
 prendra la valeur 1 si et seulement si au moins l'une des deux propositions
P ou Q prend la valeur 1.
prendra la valeur 1 si et seulement si au moins l'une des deux propositions
P ou Q prend la valeur 1.
-
| P |
Q |
 |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
1 |
Logique des propositions - 2 - tables de vérité 2
⇒ et ⇔ peuvent se définir à partir des 3 premiers opérateurs.
| A => B |
A |
B |
¬A |
¬A /\ B |
| 1 |
0 |
0 |
1 |
1 |
| 1 |
0 |
1 |
1 |
1 |
| 0 |
1 |
0 |
0 |
0 |
| 1 |
1 |
1 |
0 |
1 |
De même :
- ∧ se définit à partir de ∨ et ¬
- ∨ se définit à partir de ∧ et ¬
- etc , par exemple : Fonction_NON-ET
Logique des propositions - 3 - exemples
Les puits créent un courant d'air dans les carrés adjacents :
B1,1 ↔ (P1,2 ∨ P2,1)
B2,1 ↔ (P1,1 ∨ P2,2 ∨ P3,1)
etc pour tous les carrés.
Logique des propositions - 4 - raisonnement 2
Règle
de résolution ou principe de résolution de Robinson
A partir de G et H :
G = G1∨ G2 ∨ … ∨ Gn
H = ¬G1 ∨ H2 ∨ … ∨ Hm
on déduit K , le résolvant de G et H
K = G2 ∨ … ∨ Gn ∨ H2 ∨ … ∨ Hm
En effet ceci est toujours vrai (c à d. une tautologie ):
G1 ∨¬G1
Logique des propositions - 4 - raisonnement 3
Exemple concret avec résolution:
S ∨ T → P (1)
S ∨ R (2)
¬R (3)
on veut montrer : P .
On transforme (1):
S → P ∧ T → P
puis ramène à une forme normale:
¬S ∨ P (4)
¬T ∨ P
le résolvant de (2) et (3) est :
S (5)
le résolvant de (5) et (4) est :
P
La négation de la conséquence cherchée donne
¬P
Enfin P et ¬P donnent la clause vide.
Exemples avec Prover9
Assomptions Prover9 :
man(x) -> mortal(x). % variable x universelle par défaut
man(socrates).
But:
mortal(socrates).
Assomptions Prover9 :
all x all p all gp (
parent(x,p) & parent(p,gp)
-> grandparent(x, gp)
).
all x (
human(x) -> exists p ( parent(x,p) & human(p) ) )
But Prover9 :
human(x) -> exists gp grandparent(x,gp).
Modélisation en logique des propositions
- Tout ce qu'on exprime en SQL, UML, XML peut (et devrait) s'exprimer en
logique des propositions
et plus encore!
- et aussi la logique métier, qui est d'habitude dans un langage
informatique
Exemple: relations de famille :
male(williams) ∧
parent(williams, charles) ∧
parent(henry, charles) ∧
(
∀x ∀p ∀y parent(x,p) ∧ parent(y,p)
→ meme_parent(x,y)
)
Modélisation en logique des propositions - exemple concret
LONDRES (AFP) - L'islamiste jordanien Abou Qatada, souvent considéré comme
l'ancien bras droit de Ben Laden en Europe, a été libéré de prison mardi au
Royaume Uni.
islamiste(AbouQatada).
jordanien(AbouQatada).
∃c consideration(c). souvent(c).
au_sujet_de(c,
anciennement( bras_droit(BenLaden, Europe) = AbouQatada ) ).
∃p evenement(liberation(AbouQatada, p), mardi).
prison(p). partie_de(p, RoyaumeUni).
aujourdhui(2012-02-13).
- la plupart des "fonctions" sont des prédicats, sauf liberation et
anciennement, qui sont des fonctions au sens de la logique des
prédicats
- pas de ∀ : normal : les dépêhes expriment des faits, pas des règles
logiques
- cette transcription en logique est fidèle; pour certains usages on
aurait pu être moins précis;
il existe une méthodologie pour les systèmes experts qui part des
besoins réels: CommonKADS
- on a été amené à créer des prédicats pour des notions très
générales: evenement, partie_de
c'est l'objet des ontologies de haut niveau: Dolce, Sumo, BFO, ... voir
Famous ontologies
- il faudrait modéliser le fait que AFP est l'origine des informations
 prendra la valeur 1 si et seulement si au moins l'une des deux propositions
P ou Q prend la valeur 1.
prendra la valeur 1 si et seulement si au moins l'une des deux propositions
P ou Q prend la valeur 1.